Y-hang

[mikem]

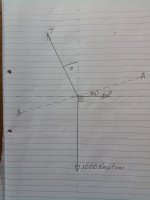
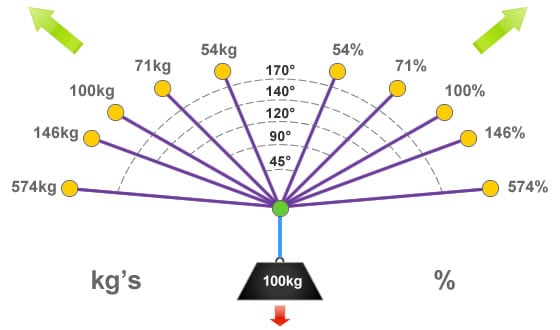
For deviations (and Y hangs) you don't really want the ropes angled at more than 60 degrees to the vertical (so 120 degrees between them), as that angle means 100% of the load on each component, there's a graph on this page showing how Y hang load increases more rapidly as angle goes beyond that:

Vector Forces - ropebook

Vector forces become apparent whenever there is an internal angle greater than 0° between two or more rigging components or anchorage points. For ease of…

www.ropebook.com

However, the angular vector forces curve for deviations is almost as if the two axes on the graph have been switched & it maxs out at 200% (see previous ropebook link), so it's not as much of an issue as for a Y. I think there's a roof deviation in Lost John's that must be more than 60 degrees?

 

[Chocolate fireguard]

The drawing is of a rope deviated by an angle "a" degrees by a horizontal deviation.
Sorry it's old tech. I'm not up to the fancy stuff.
And I've never attached anything before, so no guarantees.

The caver weighs 1000 Newtons
T represents the tension in the top section of rope which of course is the load on the main belay.
D is the deviation force to the right.

It is immediately obvious that T will be more than 1000 Newtons so long as the angle a is not zero.

The line A-----A is a line that makes an angle of a/2 degrees with the horizontal.

The analysis is familiar to many on this forum.
T cos a = 1000, so T = 1000/cos a
So for example when a is 20 degrees T will be 1000/0.94= 1064 Newtons

T sin a = D
So D = 1000 sin a/cos a and therefore D = 1000 tan a
For a 20 degree angle D will be 363 Newtons

The frictional force, F, that must be sustained by the krab/rope surface is T – 1000

The normal reaction to the surface, usually given the symbol N, is the component of D along the line A-----A, which is D cos (a/2)

The required coefficient of limiting friction for this to happen is F/N, and if the coefficient is greater the krab will stay in that position. Otherwise it will slide down the rope.

I put together an Excel spreadsheet.

a degrees	a/2 degrees	a radians	a/2 radians	cos a	cos (a/2)	tan a	F Newtons	N Newtons	Required coefficient F/N
5.00	2.50	0.09	0.04	1.00	1.00	0.09	3.82	87.41	0.04
10.00	5.00	0.17	0.09	0.98	1.00	0.18	15.43	175.66	0.09
15.00	7.50	0.26	0.13	0.97	0.99	0.27	35.28	265.66	0.13
20.00	10.00	0.35	0.17	0.94	0.98	0.36	64.18	358.44	0.18
25.00	12.50	0.44	0.22	0.91	0.98	0.47	103.38	455.25	0.23
30.00	15.00	0.52	0.26	0.87	0.97	0.58	154.70	557.68	0.28
35.00	17.50	0.61	0.31	0.82	0.95	0.70	220.77	667.80	0.33
40.00	20.00	0.70	0.35	0.77	0.94	0.84	305.41	788.50	0.39
45.00	22.50	0.79	0.39	0.71	0.92	1.00	414.21	923.88	0.45
50.00	25.00	0.87	0.44	0.64	0.91	1.19	555.72	1080.10	0.51

The coefficient of friction will be different with different ropes, krabs etc. but I think is unlikely to be less than 0.2 so an angle of 20 degrees is quite possible, with the load on the main belay 6% greater than the weight of the caver.

 

[Chocolate fireguard]

If the load above and below the krab were different and the krab was frictionless, the rope would accelerate in accordance with Newtons rather persuasive First Law of Motion. Which would be interesting to experience no doubt.

I think you mean the Second Law.
The First Law deals with the situation where there is no net force.

 

[Fjell]

I think you mean the Second Law.
The First Law deals with the situation where there is no net force.

The first law states that a body will remain at rest or in uniform motion unless a (net) force acts upon it. I think we are prob all hoping it remains at rest. The second law quantifies the acceleration.

The drawing is of a rope deviated by an angle "a" degrees by a horizontal deviation.
Sorry it's old tech. I'm not up to the fancy stuff.
And I've never attached anything before, so no guarantees.

The caver weighs 1000 Newtons
T represents the tension in the top section of rope which of course is the load on the main belay.
D is the deviation force to the right.
View attachment 16984
It is immediately obvious that T will be more than 1000 Newtons so long as the angle a is not zero.

The line A-----A is a line that makes an angle of a/2 degrees with the horizontal.

The analysis is familiar to many on this forum.
T cos a = 1000, so T = 1000/cos a
So for example when a is 20 degrees T will be 1000/0.94= 1064 Newtons

T sin a = D
So D = 1000 sin a/cos a and therefore D = 1000 tan a
For a 20 degree angle D will be 363 Newtons

The frictional force, F, that must be sustained by the krab/rope surface is T – 1000

The normal reaction to the surface, usually given the symbol N, is the component of D along the line A-----A, which is D cos (a/2)

The required coefficient of limiting friction for this to happen is F/N, and if the coefficient is greater the krab will stay in that position. Otherwise it will slide down the rope.

I put together an Excel spreadsheet.

a degrees	a/2 degrees	a radians	a/2 radians	cos a	cos (a/2)	tan a	F Newtons	N Newtons	Required coefficient F/N
5.00	2.50	0.09	0.04	1.00	1.00	0.09	3.82	87.41	0.04
10.00	5.00	0.17	0.09	0.98	1.00	0.18	15.43	175.66	0.09
15.00	7.50	0.26	0.13	0.97	0.99	0.27	35.28	265.66	0.13
20.00	10.00	0.35	0.17	0.94	0.98	0.36	64.18	358.44	0.18
25.00	12.50	0.44	0.22	0.91	0.98	0.47	103.38	455.25	0.23
30.00	15.00	0.52	0.26	0.87	0.97	0.58	154.70	557.68	0.28
35.00	17.50	0.61	0.31	0.82	0.95	0.70	220.77	667.80	0.33
40.00	20.00	0.70	0.35	0.77	0.94	0.84	305.41	788.50	0.39
45.00	22.50	0.79	0.39	0.71	0.92	1.00	414.21	923.88	0.45
50.00	25.00	0.87	0.44	0.64	0.91	1.19	555.72	1080.10	0.51

The coefficient of friction will be different with different ropes, krabs etc. but I think is unlikely to be less than 0.2 so an angle of 20 degrees is quite possible, with the load on the main belay 6% greater than the weight of the caver.

No. It‘s a rope. Imagine the krab is a pulley on a crane or something. It doesn’t matter what angle you pull at, T is always 1000 if there is no friction. Otherwise the rope would accelerate (Newtons First Law). If there is friction then T is higher than 1000 if you pull it up, and lower if you lowered it. We are in the situation of either lowering or no effect. So T is 1000 or less.

What does change is the force on the pulley or krab. Which is a reaction force. If you were lowering from below it would be 2000.

 

[mikem]

Actually Chocolate Fireguard & Chris are right, if you push the krab up then the main load increases (in above case reading goes up to 5kg) [& the scales do work properly at an angle, as it passes through 4kg when deviation is in the "neutral" position] Note the percentage change will not be as high for a person, as the friction isn't proportional to the weight difference.

 

[ChrisB]

It doesn’t matter what angle you pull at, T is always 1000 if there is no friction.

That's true, but Chocolate Fireguard's analysis assumes there is friction

The frictional force, F, that must be sustained by the krab/rope surface is T – 1000

In a deviation there is neither lowering nor raising, the rope isn't moving through the krab unless the krab is pushed up or down the rope. If it's pushed down the rope, and stays there, friction will be holding it down and thus pulling the rope up, so T is reduced above the krab. If the krab is pushed up the rope and held up by friction, the friction is pulling down on the rope and T is increased.

This differs from a pulley on a crane or similar which is fixed in position so can't move up or down the rope. In that situation, the force on the pulley could be in any direction, whereas the deviation cord must be aligned with the force on the krab. If there's no friction, the deviation will self-align to bisect the angle of the rope and T doesn't change.

 

[mikem]

Anyway, we were initially just considering the load on the deviation anchor, which is either minimal (nobody on rope or above it) or around the figures given by Mark (person below the krab). The friction between them will increase the load (slightly) whether the krab has slid down or up.

 

[ChrisB]

The friction between them will increase the load (slightly) whether the krab has slid down or up.

Yes, friction does indeed add a small additional component to the deviation force, whether up or down. If the krab has moved up, however, the angle that the deviation is turning the rope through increases, so the force on the deviation anchor goes up more, significantly more if the angle is already large. If the krab has moved down, the rope become straighter and less force is required to deviate it.