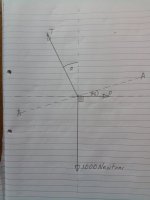
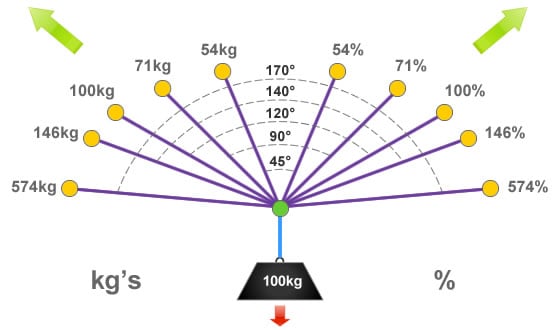
For deviations (and Y hangs) you don't really want the ropes angled at more than 60 degrees to the vertical (so 120 degrees between them), as that angle means 100% of the load on each component, there's a graph on this page showing how Y hang load increases more rapidly as angle goes beyond that:
 www.ropebook.com
www.ropebook.com
However, the angular vector forces curve for deviations is almost as if the two axes on the graph have been switched & it maxs out at 200% (see previous ropebook link), so it's not as much of an issue as for a Y. I think there's a roof deviation in Lost John's that must be more than 60 degrees?

Vector Forces - ropebook
Vector forces become apparent whenever there is an internal angle greater than 0° between two or more rigging components or anchorage points. For ease of…
 www.ropebook.com
www.ropebook.com
However, the angular vector forces curve for deviations is almost as if the two axes on the graph have been switched & it maxs out at 200% (see previous ropebook link), so it's not as much of an issue as for a Y. I think there's a roof deviation in Lost John's that must be more than 60 degrees?