Y-hang

[cap n chris]

Y hangs do lead to much nicer hangs on quite a few pitches. Eg getting the rope away from the rock.

If it's been a while since you've had a properly deep sigh here's something to help you achieve one:

Also any photo of a y-hang rigged from an RSJ or scaffold structure would count. I've long imagined that the photo above is from a "how not to make things easier/better/nicer/safer/more efficient" training manual. The traverse alone brings me out in hives. Anyhoo, cider and bed time beckons..

 

[JoshW]

If it's been a while since you've had a properly deep sigh here's something to help you achieve one: View attachment 16868
Also any photo of a y-hang rigged from an RSJ or scaffold structure would count. I've long imagined that the photo above is from a "how not to make things easier/better/nicer/safer/more efficient" training manual. The traverse alone brings me out in hives. Anyhoo, cider and bed time beckons..

That pitch (for SRT) screams for a simple deviation to the far wall.

For leading groups (ladder/lifeline) this isn’t the worst I’ve seen I’ve generally gone for a y hang off the left hand wall and dealt the the fact the lifeline rubs against the wall

 

[cap n chris]

I/we favour two independent deviations (which meet equally at the same place) from 2 independent bolts (visible on the RHS); saves about 8m of rope and mahoosive epicness for newbies.

 

[Fulk]

Better???

 

[Ian P]

I/we favour two independent deviations (which meet equally at the same place) from 2 independent bolts (visible on the RHS); saves about 8m of rope and mahoosive epicness for newbies.

I/we prefer to use the RHS as our preferred route full stop. Saves well over 8m of rope and any deviation “epicness” at all.

A really simple traverse to a really simple pitch head. No deviations required at all.

With novices, the LHS anchors can be used by the experienced caver to offer words of comfort and encouragement.

Each to their own I guess.

 

[cap n chris]

Better???

Significantly, yes. I prefer two deviations in case one fails (as the resultant rope rub would be egregious) but as Andy Sparrow once famously put it "Anything that can go wrong probably won't"

 

[langcliffe]

Better???

Nice rigging, nice snap!

 

[Fulk]

With regard to the points made by Ian – 'Each to his own', to be sure – but in a situation like that I find that because I'm right-handed rigging on the LHS is easier than rigging on the RHS, though the final descent may be better on the right.

With regard to the points made by the captain, well, to have two deviations really is a luxury; and what is the loading on a deviation anyway?

 

[mikem]

Loading on a deviation is often more than for a Y hang, as it usually rides up the rope to a higher angle, & you end up pulling outwards on the bolt rather than down.

 

[Mark Wright]

and what is the loading on a deviation anyway?

 

[Fulk]

Thanks Mark – there's food for thought there!

 

[topcat]

As above posts. The only exception being really really tight pitch heads where hangs off one wall, with rope rub , are necessary. But even there it could be a double anchor, ie Y hang off the same wall rather than a classic Y hang floating in the shaft, more or less centrally. ( as we know, some Y hangs have to be off set).

 

[topcat]

As above posts. The only exception being really really tight pitch heads where hangs off one wall, with rope rub , are necessary. But even there it could be a double anchor, ie Y hang off the same wall rather than a classic Y hang floating in the shaft, more or less centrally. ( as we know, some Y hangs have to be off set).

Sorry, this ^ post is a bit out of sequence: I hadn't spotted the fact that there was another page of posts....I was referring to 'are Y hangs even required now we have resin anchors 'bit.....

The deviation chart is interesting. Note how the load figures are quite high, then suddenly drop by a large amount.
There is a school of thought that deviations can be a bit marginal because the loads are low. But it seems often not as low as we might have thought.

I take the view that deviations are there for good reason and if they fail it is not good. In some cases deviation failure could be instantly very serious, like ending up under a waterfall.

 

[mikem]

Here's a good explanation of vector forces in deviations (& comparison at bottom to Y hangs). Of course this is for theoretical frictionless systems, whilst using a karabiner creates friction (this is why a lighter person can belay a heavier one whilst climbing), so load on main anchor will actually reduce further from 100% as the rope bends more (& presumably the share of deviation increases), but we don't really need to worry about that:

Angular Vector Forces - ropebook

Angular vector forces occur when ropes are passed through a deviation or a directional pulley. Dependent on the angle created, this can have a multiplying…

www.ropebook.com

 

[mikem]

The deviation chart is interesting. Note how the load figures are quite high, then suddenly drop by a large amount.

That is more a factor of the limited angles shown, & them not being equally spaced. For each 5 degree increase at low deviations you add c.8.7 to previous %, by 45 degrees you are adding 8.1, by 90 degrees c.6.2, 135 degrees c.3.1, & only 0.2 at 180 (0*=0%, 45*=76.5%, 90*=141.4% (so +64.9 on previous), 135*=184.8% (+43.4), 180*=200% (+15.2); using * as I can't be bothered to search out degree symbol)

 

[ChrisB]

Of course this is for theoretical frictionless systems, whilst using a karabiner creates friction … … so load on main anchor will actually reduce further from 100% as the rope bends more (& presumably the share of deviation increases)

Friction will only change the load on the anchors if the rope is moving through the krab, for example, in a hoist system. A static system has to be in equilibrium, so the load is only dependent on the relative angle of the ropes. Friction does mean that the position of the krab on the main rope can vary but, for a given position, the static forces only depend on angle.

 

[topcat]

That is more a factor of the limited angles shown, & them not being equally spaced. For each 5 degree increase at low deviations you add c.8.7 to previous %, by 45 degrees you are adding 8.1, by 90 degrees c.6.2, 135 degrees c.3.1, & only 0.2 at 180 (0*=0%, 45*=76.5%, 90*=141.4% (so +64.9 on previous), 135*=184.8% (+43.4), 180*=200% (+15.2); using * as I can't be bothered to search out degree symbol)

I did wonder about that but my tame math-magician is in swanning around Europe just now, so thanks for taking the time to illuminate

 

[Chocolate fireguard]

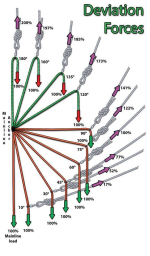
The diagram in Mark’s post #90 is for negligible friction, eg a good pulley.

It sets itself up with the line of the devi cord bisecting the angle formed by the 2 sections of the main rope, the tension in those 2 parts being equal, and equal to the weight of the caver. So that is the load on the main belay.

For an angle of 60 degrees the tension in the devi cord is the same.

As has been pointed out in ChrisB’s post #96, friction allows the krab to be positioned differently, within limits.

When approaching from below it is common practice (by me anyway) to push the krab upwards before unclipping it to make it easier to reclip after passing the deviation.

The frictional force holding it in this higher position means that the top section of rope is applying a pulling force on the krab, which is therefore pulling down on the rope, so the tension is increased by this amount, as is the load on the main belay.

This website

https://overtheedgerescue.com/rope-rescue/pulley-vesus-carabiner-efficiency/

suggests that the efficiency of a krab when used as a pulley to divert the force by 180 degrees is around the 53% mark. That seems to be for sliding friction, and static friction will be a bit more, but taking the value as is, it seems that 47% of the effort is lost via friction.

So perhaps for a 60 degree diversion, with one third the contact area on the krab, about 15% loss might be about right?

So on that basis friction will sustain a force of 15% of the caver’s weight and so for a heavy caver the maximum extra load on the belay will be around 150N, which is neither here nor there.

I imagine a similar argument holds for the load on the devi cord belay, but I’m finding that a bit more difficult.

 

[ChrisB]

The diagram in Mark’s post #90 is for negligible friction, eg a good pulley.

Mark’s diagram is based on the angle between the ropes. With the exception of the 180º case, friction makes no difference to the forces in the ropes. Friction or lack of it can affect the angle, but for a given angle, the forces must be the same. You could have a pulley, a krab or a Y hang knot; for the same angle of the ropes, the forces can be calculated without any knowledge of the friction.

The calculation is based on the vertical and horizontal components of the forces in each rope where they meet. At that point, all the horizontal forces must balance, and all the vertical forces must balance. That gives two equations which can be solved for the forces in the two diagonal ropes, assuming the force in the main vertical rope is known.

The calculation doesn’t work for the 180º case because there are no horizontal forces so only one static equation and the vertical force can only be calculated if the friction is known.

 

[Chocolate fireguard]

Mark’s diagram is based on the angle between the ropes. With the exception of the 180º case, friction makes no difference to the forces in the ropes. Friction or lack of it can affect the angle, but for a given angle, the forces must be the same. You could have a pulley, a krab or a Y hang knot; for the same angle of the ropes, the forces can be calculated without any knowledge of the friction.

The calculation is based on the vertical and horizontal components of the forces in each rope where they meet. At that point, all the horizontal forces must balance, and all the vertical forces must balance. That gives two equations which can be solved for the forces in the two diagonal ropes, assuming the force in the main vertical rope is known.

The calculation doesn’t work for the 180º case because there are no horizontal forces so only one static equation and the vertical force can only be calculated if the friction is known.

Everything you say is correct.
But you misunderstand the point of my post, which was to estimate the CHANGE in the tension of the top rope when the krab is pushed upwards and is retained in that position by friction.
The force does increase precisely because with the krab in the higher position the angles have changed.